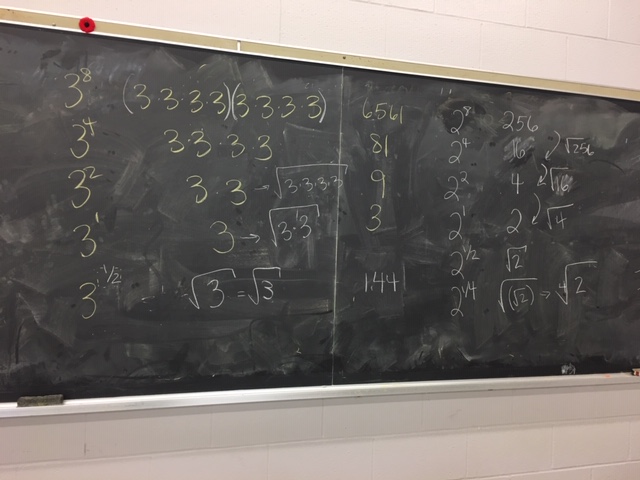Our Grade 11 Functions course is slowly becoming more of a Thinking Classroom, and one of the big shifts I’m currently working towards is Defronting the Room. I use Pear Deck regularly for setting up a problem & collecting responses (blog post to come), but this week I was looking to do a simple, oral explanation of a problem and get to the strategic thinking.
I was looking for a way to introduce rational exponents. After some failed research and culling of existing examples, I just came up with a simple problem and am sharing it here for others.
Problem

You want to get a sheet of plywood cut at Home Depot and the panel saw has a digital input to set up the dimensions (kind of a stretch, but whatever it works). The input panel has some limitations:
- No decimal numbers
- Whole numbers, fractions, and exponents are permissible
- No symbols other than what’s listed above
The crux: You want a square cut with an area of 2m2. What are the side lengths of the square?
We took some pauses throughout the problem solving to group together and look at patterning. This helped to concretize what students have already learned about exponents and also aided in solving the problem at hand. Students were challenged but were able to solve the problem, which to me is the right level of difficulty.
An extension question I used as a follow up:
Now you’re looking to make a storage cube for your house. The cube has a volume of 3m3. What are the side lengths of the cube?
It was an easy step for us then to talk about rational numbers & radical numbers and make the connections between those math terms and symbols. We did some practice in class and then students had the option to do some Khan Academy questions for extra practice.
Sometimes simple really is beautiful & just what we need for thinking deeply about math.